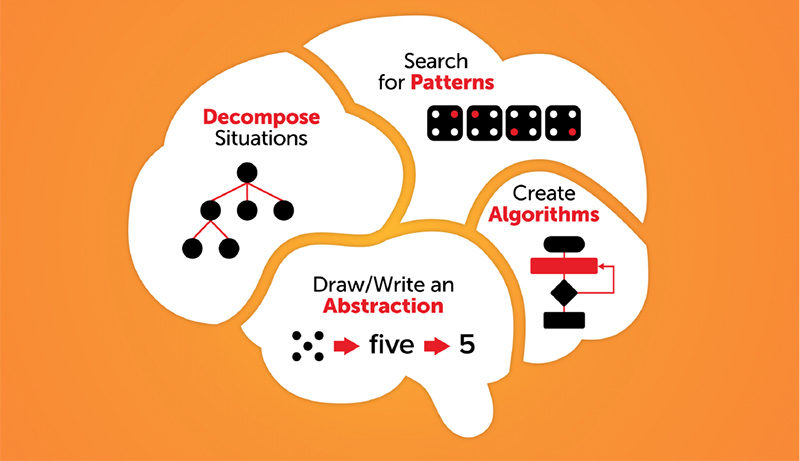
Computational Thinking: Decomposing Situations

The aim of computational thinking (CT) is to help students write “good” code for an algorithm that can be used to complete a routine sequence of steps.

The discussion here will focus on decomposing situations, one of the components of CT that were identified in my previous post.

The term algorithm is usually familiar to all adults from their years in the school when they learned how to add, subtract, multiply, or divide numbers that were beyond the range of automatic recall. It took many hours to master the sometimes meaningless steps for each of the algorithms. In almost all situations, the steps were dictated by the teacher with little explanation. The origin of the steps can be traced back to the book Liber Abaci, written in 1202 by Fibonacci. In this book, the steps are given only in words which were likely used to describe the action of beads on an abacus. Fibonacci did not create the steps; he merely summarized what was well known in the Middle East and North Africa for many centuries before 1200. The word algorithm came from the last name of the Persian Muhammad ibn-Musa al-Khwarizmi (born 780) who one of the most famous of the early non-Greek mathematicians. In a way, he and his peers were the first creators of code.

Over 1,000 years ago, the mechanics of the abacus, and later paper and pencil tools, helped to decide and refine the steps that were used for the operations. Then, like today, the mathematicians broke the process down into little steps that would work for any pair of numbers. The analysis showed that it was best to begin with place that had the least value and proceed systematically, working from right to left for most operations. The fact that the Hindu-Arabic number system had a base-ten place-value system was an important factor that helped decide the steps.

The process today of creating an algorithm is not much different from what was done long ago. Students who create algorithms need to think through all of the steps that can be used for every possible situation. Over time, students need to work toward creating algorithms that use the same and efficient sequence of steps. So, unlike mental procedures which encourage flexibility, a machine’s process is always the same.

The following situation is a very simplistic example of a sequence of steps that summarizes the thinking to create an algorithm. Pretend that a calculator is being used to find the amount that will be paid for a purchase of a number of items with a discount of 15 percent. The first portion of the sequence of steps is to add the purchase prices of the various items. The last portion involves finding and using knowledge about percentage to find the discount and the final amount that needs to be paid. So, overall the situation has been decomposed into two major segments. Note, if sales tax is included there would be a third major segment.

When the situation described above is decomposed further, the first segment involves adding a series of numbers (that is, the individual prices). A price is entered into the calculator and then a decision needs to be made: Is the plus key (+) pressed to enter another price? Or is the equal key (=) pressed to find the total? This is a decision point so in reality, we have an example of a conditional algorithm. If + is entered, the calculator will wait to receive further numbers to add. If a = is pressed, the machine will find a total.

After the machine has found the total, the second segment uses the known discount percentage to calculate the final cost. There are at least two options. One sequence of steps involves finding 15 percent (0.15) of the total, which is then subtracted from the total. This involves a multiplication followed by a subtraction. This sequence is cumbersome because after finding 15 percent of the total, the deduction must somehow be subtracted from the total. An alternate sequence of steps is to multiply the total by 85 percent, the complementary percentage to 15 percent. This can be a single straightforward calculation that does not require storing the total in the machine or your head.

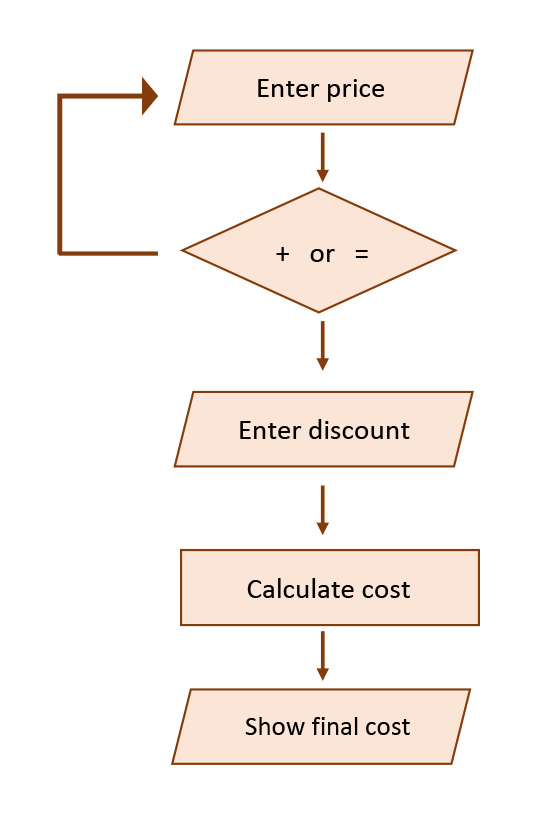
In summary, the creation of an algorithm to match a real-world situation requires very careful analysis. This involves breaking (or decomposing) the situation into individual steps that can then be used to direct a “machine” to complete the action. Generally, these steps are shown in a flowchart, like the example shown above.

Watch the recordings from our webinar series focusing on computational thinking.

• Part 1 Computational Thinking to Strengthen Elementary Mathematics: Patterning and AbstractionComputational
• Part 2 Computational Thinking to Strengthen Elementary Mathematics: Decomposition and Algorithmic Thinking
  

Click here to view the recordings.