Focus on Fractions: The Necessary Prerequisite for Addition and Subtraction of Fractions

This is part of a series on fractions. Click here for the previous article in the series.

It’s not always “apples to apples” for the addition and subtraction of fractions.

There are only a few things this writer remembers from his early elementary school days. Mrs. Weeks, my first-grade teacher, often repeated the statement, “You can only add apples to apples.” At the time, it really wasn’t clear what the “apples to apples” statement meant, but the meaning is highly relevant for adding and subtracting fractions.

Before students begin to add and subtract fractions, they have likely spent too much time completing calculations with what can be called “naked numbers.” In particular, they add or subtract whole numbers without any reference to the everyday units that are involved. For example, they add 357 + 268 without knowing if either number refers to dollars, people, cars, meters, or so on. Similarly, the work with fractions launches straight into examples like those shown below, without ensuring students have the necessary background understandings.

There are two key understandings that will help students be successful when they add/subtract fractions. These are:

1. work with fractions to focus on the units being added/subtracted, and
2. the ability to confidently find equivalent fractions.

Mrs. Weeks’s reminder that the units must be the same (“apples to apples”), is appropriate for adding and subtracting fractions. In the apples analogy, an addition equation might be written as:

3 apples + 1 apple = __ apples

So, the fraction equation above could be written as:

3 eighths + 1 eighth = __ eighths

In this case, the units are not so much everyday objects but mathematical entities. If equations that use “fractions in words” are presented to students, they see that the numerators are added and the denominators indicate the unit, so they are not added. This avoids the erroneous approach that some students use to add everything — numerators and denominators — when they begin to apply operations to fractions.

When equations like the example above are written in words, it helps to show students that two fractions cannot be added until the units (denominators) are the same. This can sometimes mean rewriting the equation:

3 fourths + 3 eighths = ___ (?)

So, rather than simply telling students that the denominators must be the same, they see the reason behind this statement.

The length model allows students to easily work with fractions greater than one whole, so it is better than either the set or area model. It is also more flexible and easier to use than the number line, as the length model is a tool that can be folded and used to construct fraction walls.

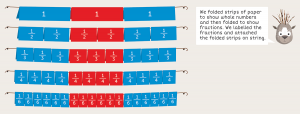
On the fraction wall below, students can see that 3 fourths (the red line) can be expressed using other units, so the word sentence and the addition equation can be rewritten in terms of eighths.

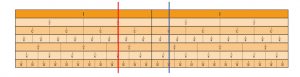
The fraction wall also makes it easy to find the sum of the two fractions (the blue line).

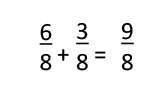
Gradually, students learn how they can use multiplication (and eventually division) to find equivalent fractions. The two rows below are from a multiplication chart.

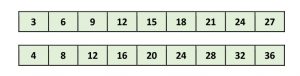
One strip can be placed just above the other to create a fraction such as ¾, as shown on the left of the two rows below. The other a/b numbers are fractions which are equivalent to ¾.

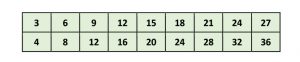
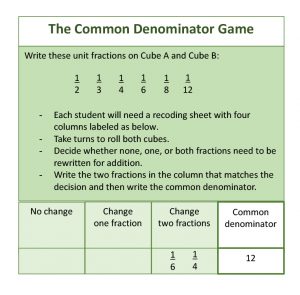
Students need to be able to fluently recall equivalent fractions. So, after the initial work with tools like a fraction wall, there needs to be frequent practice for students to quickly find pairs of equivalent fractions. Drill-and-skill work through games will help motivate students to improve fluency in equivalent fractions. Here is a simple game that can be used to help students decide what denominator should be used to create equivalent fractions. The game reinforces the idea that none, one, or both denominators may need to change.

If you recall in Are Fractions Key to a Child’s Future Success in Mathematics? many instances in mathematics, other than addition and subtraction, require students to be able to confidently recall equivalent fractions. So, as a final comment, the importance of this work cannot be understated.