5 Tips for Teaching the Use-Doubles Strategy

Ever feel like you’re seeing double? Well, if you’re teaching about doubles, then you definitely are! As students develop number fluency, it is important for them to learn the skill of adding doubles and near doubles. At ORIGO, we recommended teaching the use-doubles strategy for addition, as demonstrated in this ORIGO One video. Some refer to this as the near doubles strategy.

Keep in mind that students may initially have some difficulty understanding the use-doubles strategy for addition. This method requires a strong grasp of numbers and the ability to decompose and put them together in various ways. But don’t worry, awesome educators! There are plenty of engaging and simple ways to help students conquer this strategy and use it effectively. Here are five tips to get you started! 

Practice with small numbers first

Begin by having students practice adding doubles and near doubles of single-digit numbers before moving on to larger numbers. This will help build their confidence and understanding of the strategy. Eventually, students should be able to use this strategy with multi-digit numbers (i.e., 15 + 15) and numbers ending with zero (i.e., 600 + 700). Practice the concept and skill of decomposing numbers by having students show multiple ways to make a number (i.e. 6 can be a combination of 3+3, 4+2, 5+1, etc.). This will aid students in decomposing numbers when adding near doubles. For example, if a student knows that 7+7=14, they can also show that 7+8=15 because they know that 7+8 is the same as 7+7+1. 

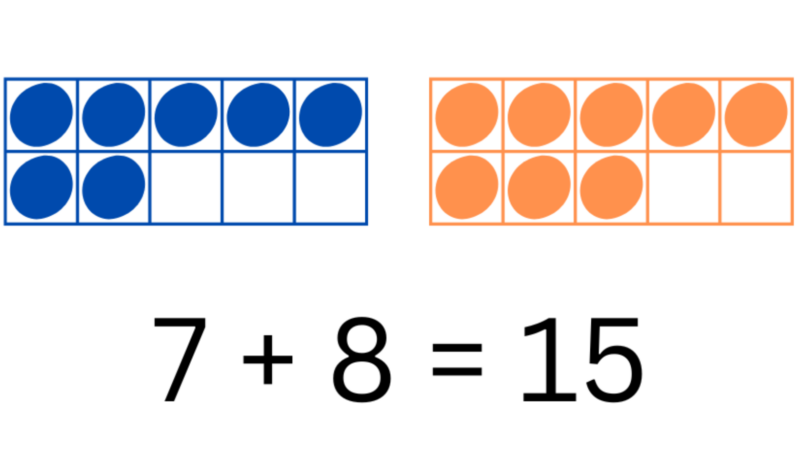
Build a foundation for addition with manipulatives

Start by giving students a hands-on understanding of adding doubles and near doubles with manipulatives. This will solidify the concept before moving on to more abstract representations.

• Use a double-ten frame with unifix cubes, snap cubes, plastic counters, or beans. These tools allow students to clearly see where the quantities are the same. For doubles facts (e.g., 3 + 3), students can fill one side of the ten frame with one color and the other side with the same color, demonstrating the equal parts.  For near doubles facts (e.g., 3 + 4), use two colors to differentiate the addends, making it easier to visually identify the “one more” addition needed to reach the sum.

• Take the learning a step further and involve student movement. Younger learners can physically represent doubles with their hands. For example, to show 2 + 2, hold up two fingers on each hand. As the numbers increase, students can work with partners. This kinesthetic approach provides a strong foundation for understanding addition concepts.

Represent the use-doubles strategy in a pictorial way using visual aids

Utilize picture cards, dominoes, number lines, double-ten frames with squares colored in, charts, or other visual aids to help students see the relationship between numbers and how the use-doubles strategy works. These pictorial aids can make the concept easier to grasp before moving on to the abstract level, where only numbers are used. 

• Use a number line to show that if addends have a difference of two, just double the number between them to get the sum. For example, 4 + 6 = 5 + 5 = 10 and 27 + 29 = 28 + 28 = 56.
• Advise students to decompose the larger number when adding near doubles. To practice this skill, students can draw a v shape underneath the number that needs to be decomposed to show what two numbers make up that number. This will help students continue to understand the use-doubles strategy at the abstract level when only symbols (i.e., written numbers) are utilized. 

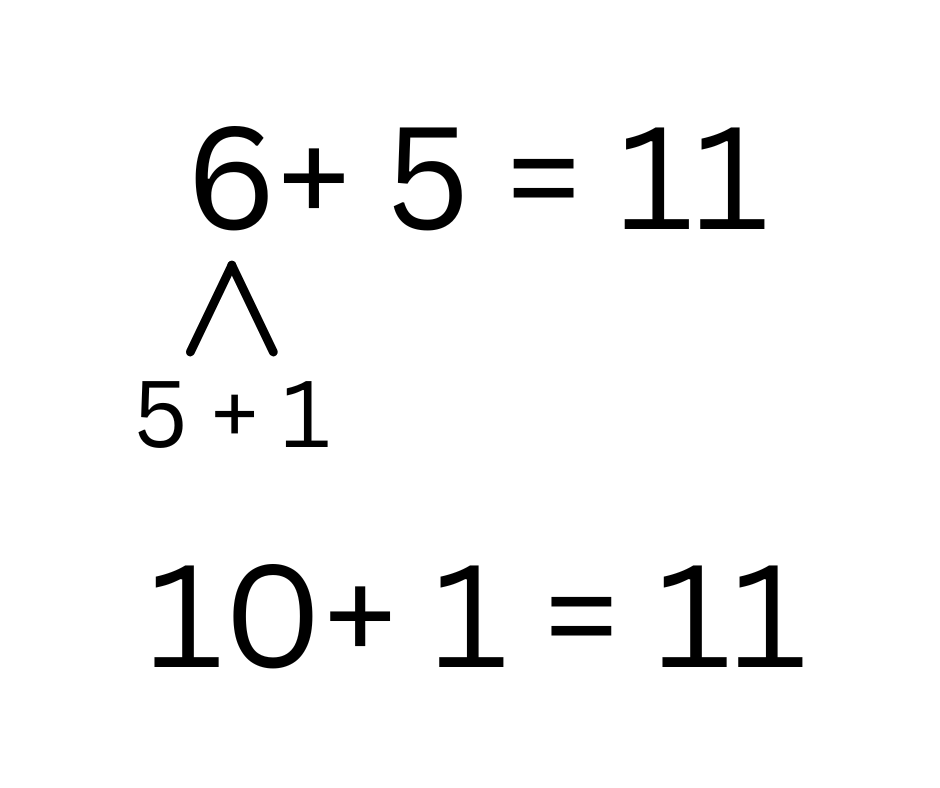
Provide opportunities for application

Give students real-world word problems or scenarios where they can apply the use-doubles strategy. This will help them see the practical relevance of the strategy and how it can be used in everyday situations. Encourage them to write out the equation. This helps them identify the numbers and see that they are doubles or near doubles. 

• If a car has two tires on each side, how many tires does it have all together? If you need to buy a spare tire, how many tires will you need in total for the car? 
• You have five fingers on each hand. How many fingers do you have altogether? 
• If you have a carton with six eggs in it and you buy another carton with six eggs in it, how many eggs do you have in total? 
• Four birds were sitting in a tree. Five more flew over and joined them. How many birds are in the tree now? 
• A spider has eight legs. If you see another spider with the same number of legs, how many legs do they have altogether? 
• Seven kids were playing on the playground. Eight more showed up. How many kids are playing now? 
• Mom is making cupcakes for the birthday party. The recipe makes twelve cupcakes, but she needs double that amount. How many cupcakes does she need to make?

By using the use-doubles strategy, students can quickly solve these real-world problems by recognizing that they already know the answer to each addition sentence because they are doubles or near doubles. This can help students build a strong foundation in basic math concepts and see how they can be applied in everyday situations.

Encourage mental math

Once students have a strong understanding of the use-doubles strategy, encourage them to practice using it mentally. This can help improve their mental math skills and make the strategy more automatic for them to use in the future. Music is a great way to improve mental math skills as the repeated lyrics and catchy tunes get stuck in your head.

Check out these videos:

Doubles Addition Facts Song | Doubles Shuffle | Math Notes with Rocko
Adding Doubles | Doubles Addition Facts Song
DOUBLES! DOUBLES! (*new* 1-10 version)
Doubles Plus One (1-5)

Here are some other doubles and near-doubles activities for you to explore: 

5-simple-and-effective-ways-to-practice-doubles-facts-in-math

Extending the Doubles and Near Doubles Facts: An Addition Strategy – Shelley Gray

3 Activities to Make Doubles Addition Fun {+ FREEBIE}

The use-doubles strategy is included in The Book and Box of Facts: Addition and Subtraction.

This strategy can also be used for doubles in multiplication, as shown in this ORIGO One video. Use these strategies to help your students develop their number fluency and mental calculation skills!