Visual Models in Mathematics: The First Classroom Examples (Part 2)

This article is the second in a four-part series on Visual Models in Math. Read this post and check out the other articles in our series:

• Part 1: Visual Models in Mathematics: Numerals – The First Images (Part 1)
• Part 2: Visual Models in Mathematics: The First Classroom Examples (Part 2 – this post)
• Part 3: Visual Models in Mathematics: The Importance of a Number Line (Part 3)
• Part 4: Visual Models in Mathematics: Graphic Organizers That Accelerate Learning (Part 4)

What Is a Visual Model in Math?

A math visual model consists of materials (mostly with pictures or images) to help interpret the numbers. Using visual materials and manipulatives as classroom math models took time to develop.

Elementary Mathematics Textbooks

In 1821 Warren Colburn published the first arithmetic book that was designed to be used with students of elementary school age. Because of the earlier age of the learners, his approach to instruction stressed the use of concrete and manipulative materials, collectively called practical materials. His methodology was based on a plan devised by Pestalozzi, a German philosopher. The preface to Colburn’s book describes the steps to be used in a general way, but the selection of the materials is left to the teacher. Interestingly, Colburn advocated the delay of drill until after understanding.¹

The use of practical materials meant that much of the teaching throughout the next 150 years involved what could collectively be called “shopkeepers’ mathematics.” The term “shopkeeper” applied to rural pursuits, trades, or sales. The most popular books throughout this period were filled with problems which involved geometry and measurement (including money). The nature of the content meant that it was natural and necessary to use visual models in math. If a situation required any calculation, the expectation was first and foremost to use mental methods.

In the 1800s, the content of elementary school mathematics to be taught was provided in one or two books. As the percentage of the population who attended elementary school increased, there was a parallel increase in the number of books used across the grades to teach mathematics. By the late 1940s, the elementary schools were bursting with students, one mathematics book was used per grade (and per pupil as a matter of necessity for the teacher), and the only “practical” examples were shown in books. Concrete and manipulative materials in the classroom did not exist.

Era of New Math

During the era of new math (the 1960s), which I studied and then taught, the teaching of numbers in other bases was used to highlight the place value structure of Hindu-Arabic numbers. (See previous article on the first images used in mathematics.) While a study of base two might have been beneficial for the looming computer era, most of this work involved meaningless conversions. However, materials (mostly with pictures) recommended that we use multi-base arithmetic blocks (or images) to help interpret the numbers. I became interested and explored the use of these manipulatives further. My research indicated the origin of this material was likely Maria Montessori who used beads like those shown to help disadvantaged children in Rome, Italy around 1900. This was probably the first of what might be called structured mathematics materials.

Photograph courtesy of Nienhuis Montessori

Modern-Day Materials

The modern-day base ten blocks, made of wood or plastic, assisted me in helping students who struggled with some of the unique features of the place value system of numbers. During our work with the blocks to represent numbers, we found that a numeral expander is a simple and effective way to help students interpret and write numbers because it links the concrete image to the abstract symbols.

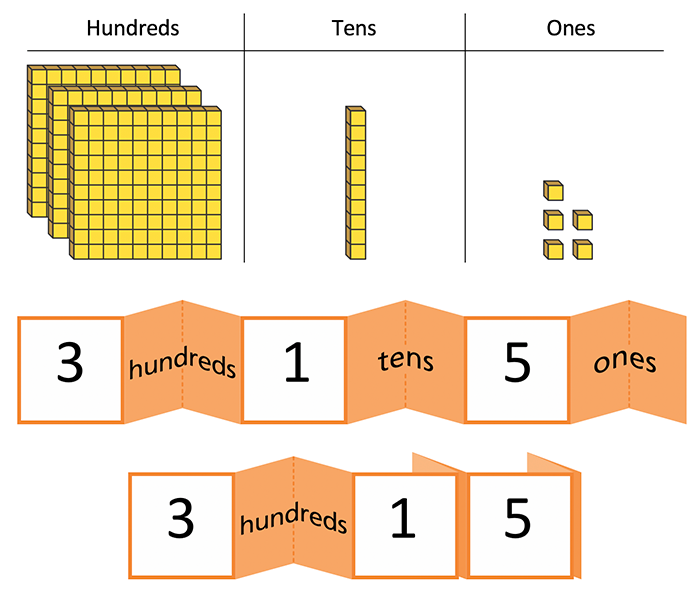
Click on the ORIGO ONE video for more about how classroom math models such as numeral expanders support operations and place value understanding. (Click on the Resource Hub link below to download a 3-digit numeral expander to use in your classroom.)

Using Numeral Expanders to Foster Thinking Skills from ORIGO Education on Vimeo.

The next blog will describe the special features of the number line that make it an essential and versatile visual model to provide understanding across a range of mathematical situations.

Reference

¹Jones, P. Coxford, A. et.al. (1970). A History of Mathematics Education in the United States and Canada. Washington: The National Council of Teachers of Mathematics. (page 105)

Click HERE for the downloadable resources for this article!

About the Author

Calvin Irons cofounded ORIGO Education with James Burnett in 1995. Cal has been involved in mathematics education for over 50 years. He started his career as a specialist teacher of mathematics in Iowa after completing his BA and MA at the University of Northern Iowa in 1967. Dr. Irons received his PhD from Indiana University in 1975 (the dissertation topic was the teaching of division). In 1975, he accepted a position at the Queensland University of Technology, Brisbane, Australia where he has been involved in the teaching and the development of mathematics curricula for elementary schools. He has received outstanding achievement awards from the university for his work and in 2014 was the student’s nominee for University Outstanding Teacher of the Year from a university faculty of over 3000 professors. He is the author/co-author of over 600 books or articles including the award-winning ORIGO Stepping Stones mathematics program.

About ORIGO Education

ORIGO Education is dedicated to making learning meaningful, enjoyable and accessible for all students and their teachers with Pre-K and Elementary print and digital instructional materials, as well as professional learning for mathematics.