The Doubling Strategy for Multiplication

The doubling strategy is great for multiplication!

What strategies could you use to solve this problem mentally? What strategies would your students use?

When I pose this problem to teachers in professional learning sessions, many mental strategies get revealed. Here are just a few that are often shared.

“Double sixteen, then double the result.”

“Multiply fifteen by four, then add four ones.”

“Add together four groups of ten and four groups of six.”

“Find four groups of twenty, then subtract four groups of four.”

We want students to think as flexibly about numbers and operations as these teachers do. Students need to demonstrate flexibility when performing mental calculations. For this multiplication problem and many others, knowing how to double efficiently is a great strategy.

Doubling is a strategy that people of all ages frequently use. Young children first learn doubles as an addition of two groups. What multiplication facts can be used by using a doubling strategy? If you said the twos, fours, and eights facts then you are correct! That’s what makes this strategy so powerful.

Fun Fact:

The word double comes from the Latin word duplus. This is a combination of duo, meaning “two,” and plus, which means “fold.” When something is folded over itself, there are twice as many layers as before.

Introduce the Doubling Strategy

Use images that help students visualize the quantities by displaying them in an array structure. The card below shows the mental picture we want students to have of two groups of six, or double six. (If students have been working with ten-frames, they might see the quantity as a ten and two more!)

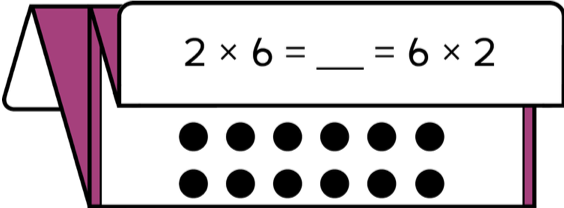
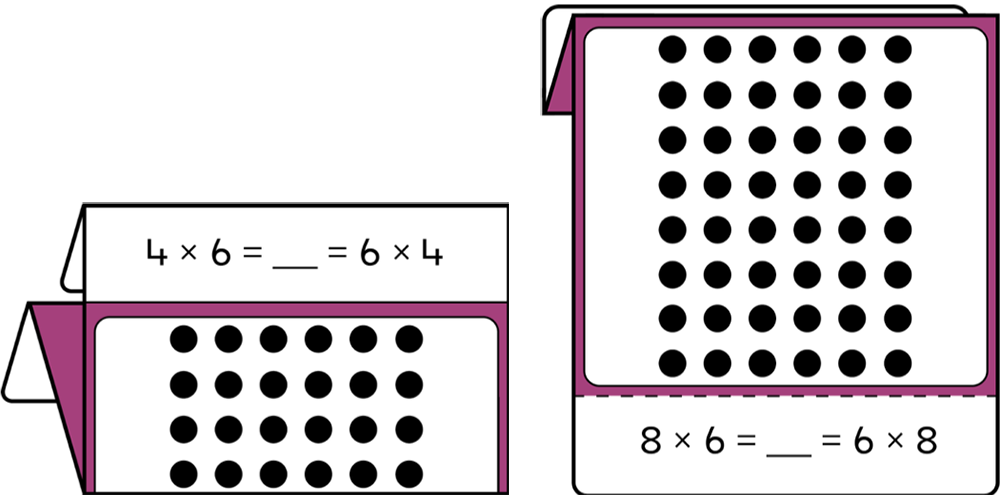
These arrays can be expanded to show the relationship between the twos, fours, and eights multiplication facts. Be sure to emphasize how the pictures show the doubling that is occurring. The turnaround facts (e.g. 4 x 6 = 6 x 4) are easily demonstrated by rotating the card 90° and by having students focus on the number or rows or the number of columns in the array.

Reinforce the Strategy

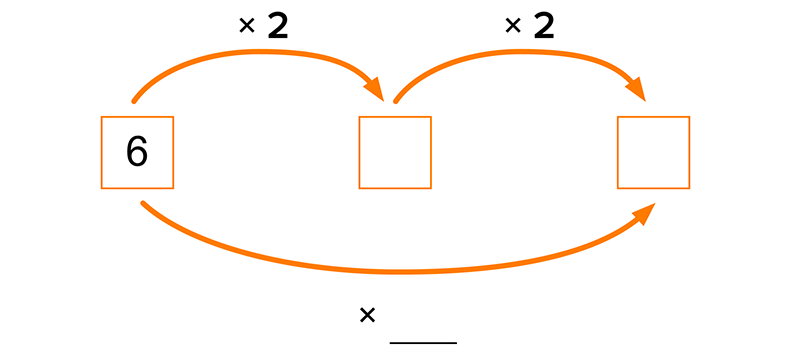
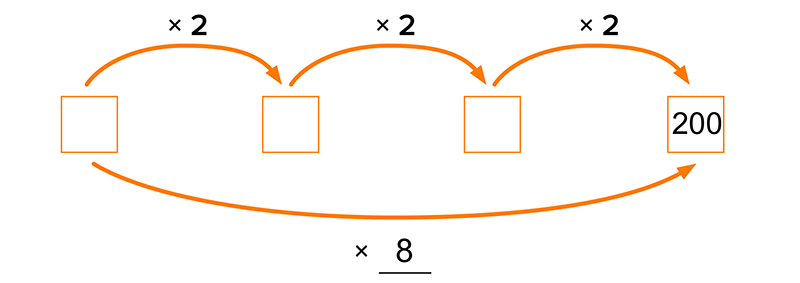
Draw the diagram shown below on the board. Ask a volunteer to write a numeral in the first box on the left. (I have provided the numeral 6 as an example.) Say, “Use the arrows to figure out what to write in the other boxes.” Challenge the students to figure out the other numbers. Encourage them to explain the thinking they used and the relationship between the three numbers. Solidify their understanding by having them write what factor they could multiply the number in the left box by to get the number in the right box.

Practice the Strategy: Multiplication Doubling Game (Free Printable Included)

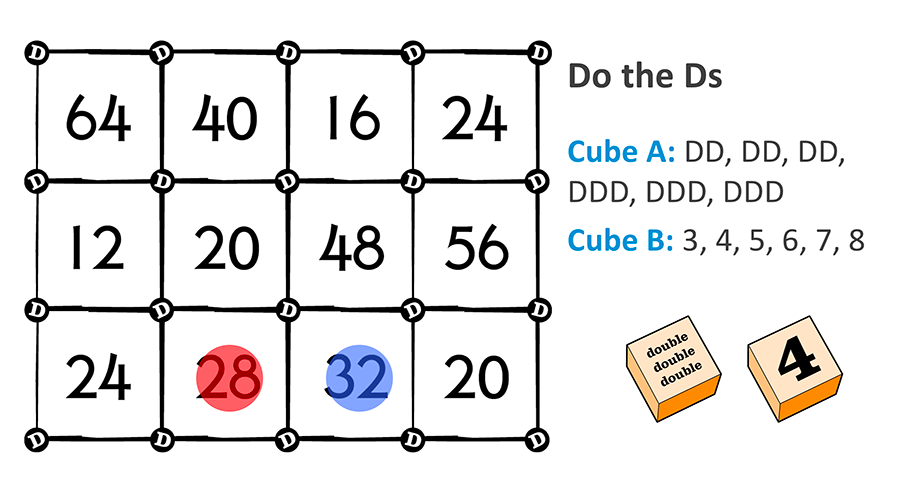
Do the Ds is a fun and easy game to practice the doubling strategy for multiplication with students.

Materials

Each group of students will need

• Do the Ds game board (click here to download the free game printable)
• 2 blank cubes, marked as follows:
  Write “double double” or “DD” on three faces, write “double double double” or “DDD” on the remaining three faces on one cube
  Write 3, 4, 5, 6, 7, 8 on the other cube.

Each player will need

• 4 transparent counters (a different color for each player)

Directions (2-4 Players)

• The first player rolls the two cubes.
• The player follows the instruction, doubling the number two or three times. Example: Lily rolls “4” and “DDD”. She thinks double 4 is 8, double 8 is 16, double 16 is 32. Four multiplied by 8 is 32.
• The player claims the answer on the game board by covering it with a counter. If an answer is unavailable, the player misses a turn.
• Each of the other players has a turn.
• The first player to place all four counters on the game board is the winner.

Example roll from Player 1. “Double 7 is 14. Double 14 is 28. Four multiplied by 7 is 28.”

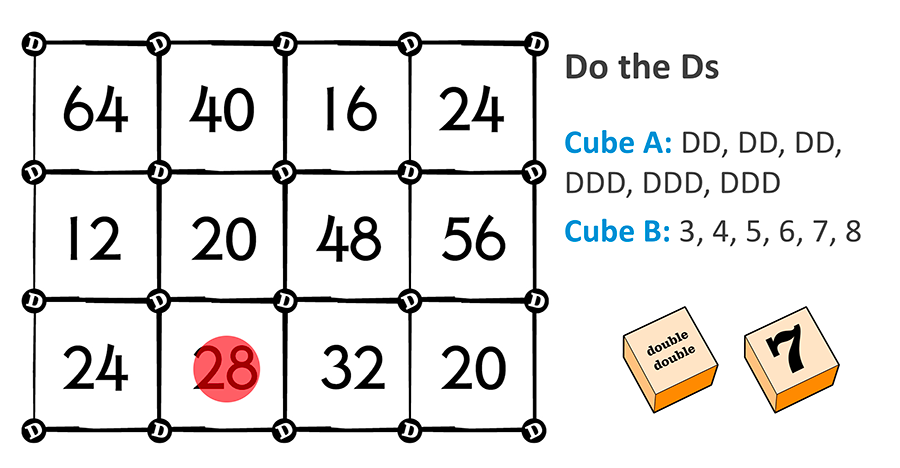
Example roll from Player 2. “Double 4 is 8. Double 8 is 16. Double 16 is 32.  Eight multiplied by 4 is 32.”

Extend the Strategy

Arrow diagrams can be extended from the fours facts to show the related eights facts. Arrow diagrams also show function relationships and are therefore useful visual models for showing the connection to the inverse operation of division.

See this ORIGO One video for more about this strategy.

Teaching the doubling strategy for multiplication from ORIGO Education on Vimeo.

The doubling strategy for multiplication is one of many important strategies included in The Box and Book of Facts for Multiplication and Division from ORIGO Education. Use this and other strategies to grow the fact fluency and mental computation power of YOUR students!

Click HERE to sign up to download the resource for this article!

About ORIGO Education

ORIGO Education is dedicated to making learning meaningful, enjoyable and accessible for all students with Pre-K and Elementary print and digital instructional materials, as well as professional learning for mathematics.