Insights

Fun and Engaging Activities for Learning Basic Multiplication and Division Facts

There are many strategies for students to use when learning basic multiplication and division facts. Here are Origo One videos and examples of several we recommend:

Use a number line for basic facts of multiplication and division

Multiplication can be repeated addition, and division is repeated subtraction. Help students understand these concepts by using a number line to demonstrate how the numbers increase or decrease in equal increments. A number line helps to visualize this process.

Consider the following multiplication problem of 4 x 5. Using a number line, students would start at zero and increase to the right on the line to show, or jump, four groups of five equal intervals, (5, 10, 15, 20), demonstrating how 4 x 5 = 20. You can also demonstrate how multiplication is repeated addition by writing +5 on a hump above each group.

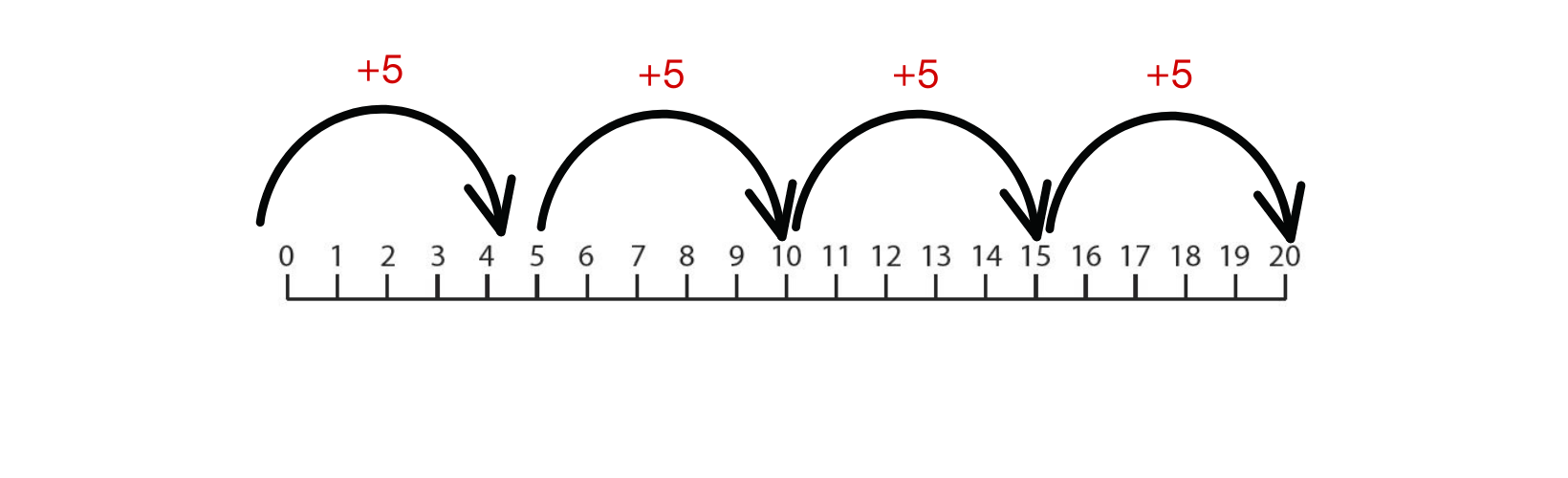
A number line can be used in two different ways when demonstrating division. For the equation 15 ÷ 3, students could start at zero and increase by three each time until reaching 15. They would count how many times they jumped to a group of three, finding that it was five times. So 15 ÷ 3 would equal 5. Or they could start at fifteen, going backward by three each time until reaching zero.

Again, they would find that it took five jumps, so the answer to the equation would be the same. Some students struggle with counting backward so the first division method could be better for them to use.

Another way to word it instead of saying “jumps” would be to ask “How many groups of 3 are in 15?”. Demonstrating that division is repeated subtraction can be shown by writing -3 over each hump when going from 15 back to 0.

Show the connection between multiplication and division

These two concepts both have to do with grouping, but are opposite ways to show that grouping.

Multiplication starts with the parts (or factors) to produce a whole (the product). Division starts with the whole (the dividend), divides it into one part (the divisor), and the answer is the other part (the quotient).

Once students understand the basic concepts of multiplication and division, practice the related facts (or fact families) together (i.e. 9 x 3 = 27, 3 x 9 = 27, 27 ÷ 3 = 9, and 27÷ 9 = 3).

Use a variety of words to describe what is happening within a multiplication or division problem. Use pictorial examples or manipulatives to demonstrate the equations.

Six times two
Six groups of two
Six multiplied by two
Be sure to show how the groups would be different if the factors were reversed using the commutative property (i.e. two groups of six)

Twelve divided by three equals four
Twelve divided/shared into three groups equals four in each group
Twelve split so there are three in each group equals four equal groups (e.g. 12 trading cards shared among 4 friends means each friend gets 3 cards).

Practice skip counting in a variety of ways to improve math fact fluency

Skip counting is a great way to demonstrate the concept that multiplication and division are equal groups of repeated addition and subtraction. Skip counting builds number fluency and memory recall.

Once students are comfortable skip counting from zero, practice skip counting starting at higher numbers they may not have memorized. For example, instead of only going up to 36 when counting by 3s, start at 48 and have them continue to skip count by threes.

While the process may be slower as they may have to begin by counting on one number at a time (49, 50, 51), it will be a good brain exercise to continue thinking about groups of 3 each time.

Use manipulatives for multiplication and division

Little boy using the base 10 method to do addition at home

These provide a way for students to combine and separate manipulatives into equal-sized groups. The physical and visual nature of manipulatives aids students in bridging the gap between abstract and concrete understanding.

For example, to demonstrate 3 x 4, students could use manipulatives to show three groups of four objects. With a division problem like 18 ÷ 6, students could divide the eighteen into groups of six showing there are three in each group. They could also divide it into groups with six in each which would result in them having 3 groups.

These activities could lead to a discussion of how to use multiplication and division facts in real life.

Teach the commutative and distributive properties of multiplication

The commutative property means that factors can be multiplied in any order to equal the same product. For example, 7 x 6 = 42 and 6 x 7 = 42.

This can be helpful for students as they learn their basic fact families because of the related facts. The distributive property helps solve problems in which a student has not memorized the facts yet or when they are solving the problem mentally.

Here is an example using the distributive property: 12 x 4 = (10 x 4) + (2 x 4) = 48. This provides a way for students to redistribute a factor into the basic facts they already know to solve the problem.

Teach divisibility rules

Divisibility Rules

Applying these rules will help students more easily solve long-division problems or factorization. They can look at a divisor and easily know which numbers it is divisible by.

Generally, when a number is divisible by another number, there will be no remainder left. Using divisibility rules removes the need for guessing random facts and going through the division process only to find you need to go much higher or lower.

Need ideas for fun and engaging activities for learning and practicing basic multiplication and division facts? Check these out!

Also, be sure to explore ORIGO’S Book and Box of Fact Strategies: Multiplication and Division.

This resource is designed to help teachers improve their students’ mathematical thinking skills and fluency with a comprehensive collection of engaging activities and visual aids in English and Spanish.