Early Childhood
Using Language Stages to Guide the Development of Measurement Concepts (Part 2)
Using Language Stages to Guide the Development of Measurement Concepts
Language can be used to guide the development of nearly all mathematics concepts including the development of measurement concepts. In fact, when language is used in the teaching of mathematics it forces curriculum planners to focus on concepts and not just skills or procedures.
To make this point, I often ask adults (pre-service or in-service teachers as well as parents) “What is area?” The response is invariably, “length by width.” This is of course a rule or procedure. Further, it is a procedure to find the area of a particular shape. So, my reaction is something like; “What does this mean for a circle?” The answer to this question is something like, “Oh, area is different for a circle.” But area is area no matter the context. So I return to my original question, “What is area?”
In the dialogue above, the word “area” could be replaced with many other mathematical terms. When I receive a reply that focuses on a rule, I know that the individual does not have a clear idea of the related concept. Rules that are remembered and applied without consideration lead to all types of misconceptions.

The table above has several measurable attributes which include – length (height or width); weight; and area (of the surface). A discussion about each attribute should bring out the key term(s) that give meaning for the related attribute or concept. For area, the language usually describes an amount of covering. This idea needs to be in the background for all activities that focus on the development of the area concept.
The chart below summarizes the 4 language stages that were introduced in my previous blog post. The examples on the right illustrate the stages with activities for area, but can be used with any measurement attribute taught in grades K–12. The language stages can be used to act as a guide to plan activities in parallel with a development that involves the typical sequence of using non-standard and then standard units. While real world settings are used throughout with these measurement concepts, the first stage is very important as it requires students to hold and compare objects without any tools (cubes, tiles, or a ruler) to measure. The initial stage focuses directly on the language of the concept being developed. Students ‘get it’ when they stand back-to-back for height/length, heft two objects (one in each hand) for weight; or put one envelope on top of another to compare the amount of covering for area. In the initial stage, the language they use starts the development of concept and in turn, how it is measured.
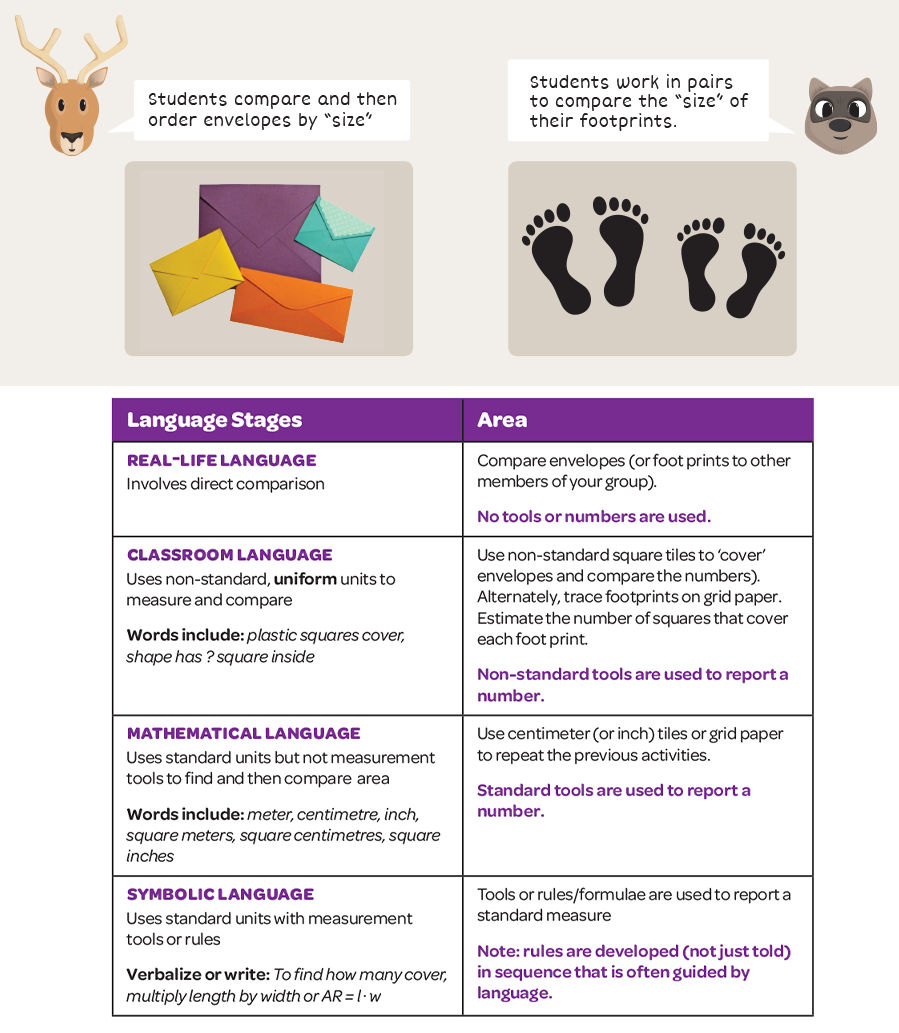
In the last stage, students use tools such as rulers, scales, measuring jugs, and clocks. For attributes such as area and volume, it is necessary to use more than a tool. Formulae and rules, which are specific to the shapes and objects involved, are required to make calculations before a number can be reported. The development of rules to calculate area also follows the language stages.
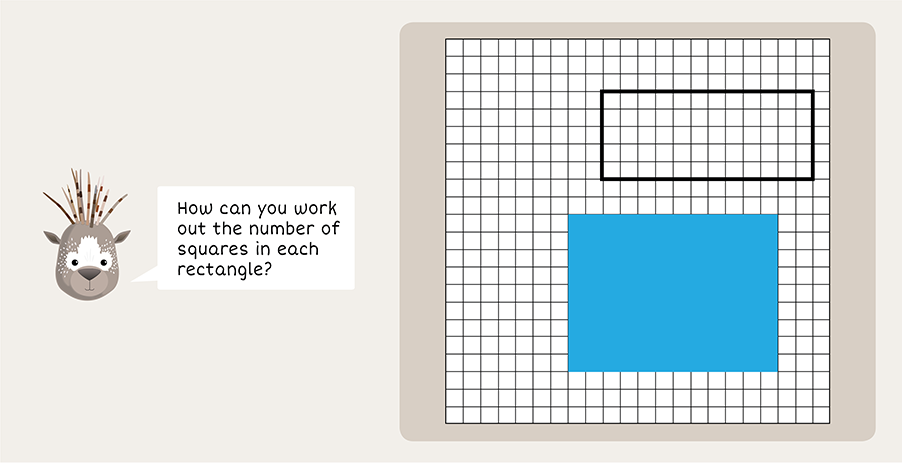
In the picture above, students are invited to describe the methods they would use. They make the connection to multiplication, but a formal rule is not written symbolically until each has been verbalized in multiple ways as it relates to the shape. The rectangle shape rule is developed initially, then the language stages are used again to establish the area rules for a square, parallelogram, triangle and finally a circle.
Note: The two activities shown above feature in the Pre-K to Grade 1 Mathematics for Young Minds – Measurement activity book from ORIGO Education, written by Rosemary and Calvin Irons.
About the Author
Calvin Irons cofounded ORIGO Education with James Burnett in 1995. Cal has been involved in mathematics education for over 50 years. He started his career as a specialist teacher of mathematics in Iowa after completing his BA and MA at the University of Northern Iowa in 1967. Dr. Irons received his PhD from Indiana University in 1975 (the dissertation topic was the teaching of division). In 1975, he accepted a position at the Queensland University of Technology, Brisbane, Australia where he has been involved in the teaching and the development of mathematics curricula for elementary schools. He has received outstanding achievement awards from the university for his work and in 2014 was the student’s nominee for University Outstanding Teacher of the Year from a university faculty of over 3000 professors. He is the author/co-author of over 600 books or articles including the award-winning ORIGO Stepping Stones mathematics program.
About ORIGO Education
ORIGO Education is dedicated to making learning mathematics meaningful, enjoyable and accessible for all, offering Pre-K through Grade 6 instructional materials, and professional learning.
![]()




