Visual Models in Mathematics: The First Images (Part 1)

This article is the first in a four-part series on Visual Models in Mathematics. Read this post and check out the other articles in our series:

• Part 1: Visual Models in Mathematics: The First Images (Part 1 – this post)
• Part 2: Visual Models in Mathematics: The First Classroom Examples (Part 2)
• Part 3: Visual Models in Mathematics: The Importance of a Number Line (Part 3)
• Part 4: Visual Models in Mathematics: Graphic Organizers That Accelerate Learning (Part 4) 

The first visual models in mathematics were numerals

Mathematics is frequently associated with symbols, number sentences, and formulae. However, the first practical examples of mathematics involved three dimensional or pictorial images that had some everyday meaning for the people working with the ideas. Symbols were not used very much. The symbols that were used usually had some connection to the world that was familiar to the user.

Counting was probably the first and most common application of mathematics. This skill is associated with fingers. Today young children (and many adults) count and uncurl their fingers as they recite the number name sequence. Numerals and fingers just seem to go together. Consequently, it is probably no accident that fingers and the numerals (zero to nine) share a common name. They are both called digits.

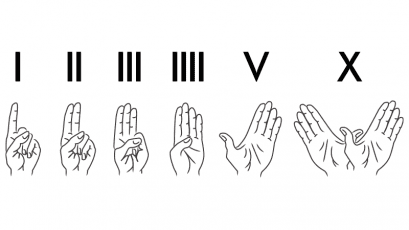
Roman Numerals

When the Romans developed their way to represent numbers, there was a close connection to the fingers and hands. The illustration below indicates how fingers were used to show one to four. (The first Roman Numerals did not involve subtraction.) The V of the hand represented five, and two hands arranged as shown meant ten.

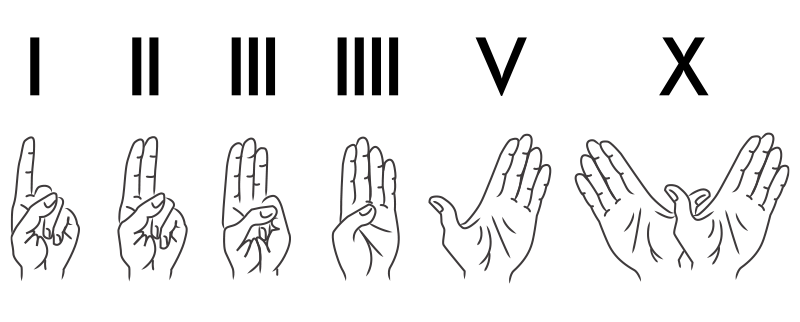
Egyptian Numerals

The Egyptians used images of everyday “things” that were related to the size of quantities they saw in their world. For example, a single stroke was one, a cattle hobble was used for ten, and the coil represented the rope with equally spaced knots they used to measure and mark out the fields. The greater numbers were linked to groups of everyday objects such as flowers, fingers (of captured slaves), and frogs. One million was a sign of amazement.

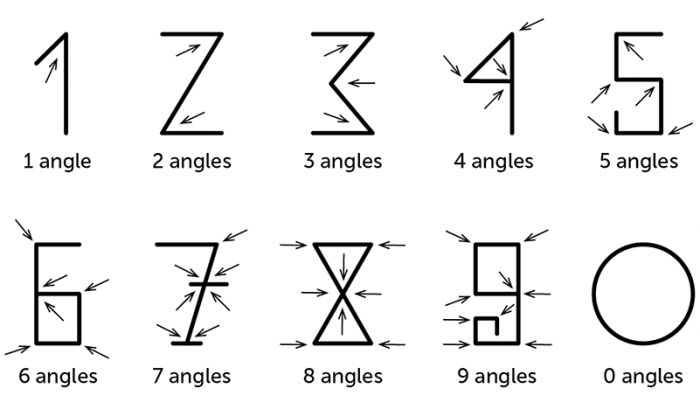
Hindu-Arabic Numerals

There is speculation about the origin of the Hindu-Arabic numerals used today. Although the examples shown below have not been verified, some people like to think that the number of angles helped to shape the numerals. The recent history of writing numerals, particularly in Europe, does support this idea. But for the moment, it is just an interesting speculation.

Brahmi Numerals

The Hindu-Arabic numerals that we use today evolved from a set of numerals known as Brahmi numerals. These numerals were used in India from around 300 BC. Here are the first nine Brahmi numerals. (Click on the Resource Hub below to download a support page on Brahmi numerals to use in your classroom.)

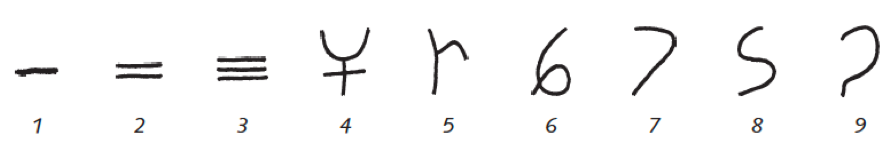
Click HERE to download the language stages poster described in the article.

About the Author

Calvin Irons cofounded ORIGO Education with James Burnett in 1995. Cal has been involved in mathematics education for over 50 years. He started his career as a specialist teacher of mathematics in Iowa after completing his BA and MA at the University of Northern Iowa in 1967.  Dr. Irons received his PhD from Indiana University in 1975 (the dissertation topic was the teaching of division). In 1975, he accepted a position at the Queensland University of Technology, Brisbane, Australia where he has been involved in the teaching and the development of mathematics curricula for elementary schools. He has received outstanding achievement awards from the university for his work and in 2014 was the student’s nominee for University Outstanding Teacher of the Year from a university faculty of over 3000 professors.  He is the author/co-author of over 600 books or articles including the award-winning ORIGO Stepping Stones mathematics program.

About ORIGO Education

ORIGO Education is dedicated to making learning meaningful, enjoyable and accessible for all students and their teachers with Pre-K and Elementary print and digital instructional materials, as well as professional learning for mathematics.