Problem-Solving: Using the Right Problem at the Right Time to Challenge Students

This article is the first in a four-part series on problem-solving.

Remember Goldilocks? She was looking for “just right” as she rummaged through the house of the three bears. As teachers, we’re also looking for “just right.” How do we offer our students mathematical challenges which are “just right?” This question applies to the classroom in many ways. Let’s consider the case of problem-solving.

Problem-solving is an important part of mathematics teaching and learning. It’s also a term which is used in many different ways in mathematics classrooms. We have word problems, rich tasks, applications of mathematics, and many others which fall under this broad umbrella. Which one is “just right” depends on our instructional purpose. What is our learning intention for our students? What sort of problem-solving task best meets this purpose?

One purpose for a problem-solving lesson is to develop students’ ease and flexibility with problem-solving strategies. What sorts of problems provide opportunities for students to practice using a variety of strategies to find the solution? Here is one example.

ORIGO Stepping Stones 2.0, Grade 2, Module 3, Problem Solving Activity 4

This problem, for students in primary grades, provides an excellent opportunity to explore problem-solving strategies.  The numbers are simple so students will not be bogged down in computation and the problem lends itself to a variety of strategies.

Another purpose for a problem-solving lesson is to connect mathematical ideas. In this case, the problem might not have the same real-world connection that the people on the bus problem has, but it pushes students to reason about the mathematics they know in order to find a solution.  This problem about partial products is one example.

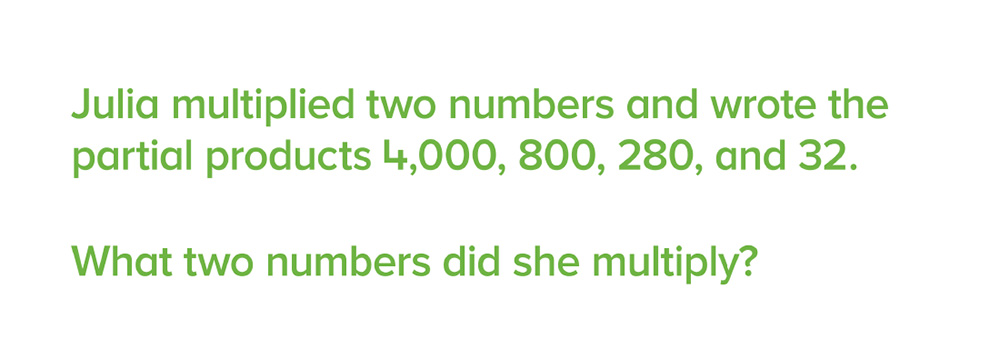
ORIGO Stepping Stones 2.0, Grade 4, Module 6, Problem Solving Activity 1

This problem encourages students to work backward (a strategy they might have developed with the bus problem) about mathematics they are currently studying.  If the product includes the four values named, what might the factors be? If you are not familiar with partial products, consider the diagram below which shows the partial products of 400, 280, and 24 for the problem 4 x 176.

ORIGO Stepping Stones 2.0, Grade 4, Lesson 6.2

Along the way, students bring together understanding of multiplication, factoring, the distributive property, basic facts, and place value.

The third purpose included here is the purpose of connecting mathematics to the real world.  “When am I ever going to have to use this?” as our students ask.  In these problems, real world connections and applications familiar to the student are critical.  There might be a range of reasonable answers depending on the approach taken to the problem.  Here is an example for you to try.

ORIGO STaRT (Student Thinking and Reasoning Tasks), Grade 4, Task 9

This problem challenges students to make sense of a problem where the facts they need to know are not clearly stated.  How many days in a year?  How many hours in a day?  How many beats in an hour?  Does your heart always beat at the same rate?  As a teacher, there is not a single correct answer.  What range of responses is reasonable?  With good justification, of course!

This post has shared three very different problems, each appropriate for a particular instructional purpose.  As you search for the problem which is “just right” for your students, consider these questions:

• What is your instructional purpose?
• How difficult and how complex is the problem? Are the numbers friendly or more challenging?  Is the situation clearly defined or messy?
• What problem-solving strategies are students confident about?

In the next post for this series, we will look more deeply into problem-solving strategies.  What are common strategies students often use?  How do we develop these strategies from student work? Future posts will address the classroom environment for problem-solving.

If you would like to explore these ideas further, please watch this edWeb webinar about this topic. You’ll see example approaches to the problems included here as well as additional research and information about this topic.

To download the resource for this blog post, please click HERE.

About ORIGO Education

ORIGO Education is dedicated to making learning meaningful, enjoyable and accessible for all students with Pre-K and Elementary print and digital instructional materials, as well as professional learning for mathematics.