Multiplication and Division
4 Strategies for Multiplication and Division Fluency
We all want our students to be fluent in multiplication and division, but what does fluency in mathematics mean? Students are fluent when they:
• Demonstrate flexibility in the computational methods they choose,
• Can understand and explain their methods, and
• Produce accurate answers efficiently.
Let’s unpack that.
Demonstrate flexibility: Students have several strategies from which to choose and they are able to select the strategy that best meets the challenges of the problem they are solving.
Understand and explain a method: Students are able to discuss why they chose a particular strategy (and perhaps why they discarded others) and how they used it to arrive at an answer.
Produce accurate answers efficiently: Students must be able to arrive at an accurate answer in a reasonable amount of time. Although speed is not the goal, a rule of thumb to use for efficiency is 3–5 seconds per fact.
So, fluency starts with providing students with a range of strategies they can use to understand the math behind the problem. The best strategies are:
• Flexible/Generalizable: The strategy can be varied, or extended, and used with greater numbers
• Efficient: The strategy has only a few steps
• Accurate: The strategy yields the correct answer every time
When we talk about fluency, we are in essence providing students with a toolkit of strategies they can use to solve any math problem they encounter, in this case strategies that help them multiply and divide accurately and efficiently.
Doubling & Halving
Doubling is a great strategy to start with, since kids most likely have used this strategy already for addition problems: 2 + 2, 3 + 3, 4 + 4, etc. So double 2 is 4, double 3 is 6, double 4 is 8, and so on. And then you can double, double (or multiply by 4) or double, double, double (or multiply by 8) as the illustration below shows.
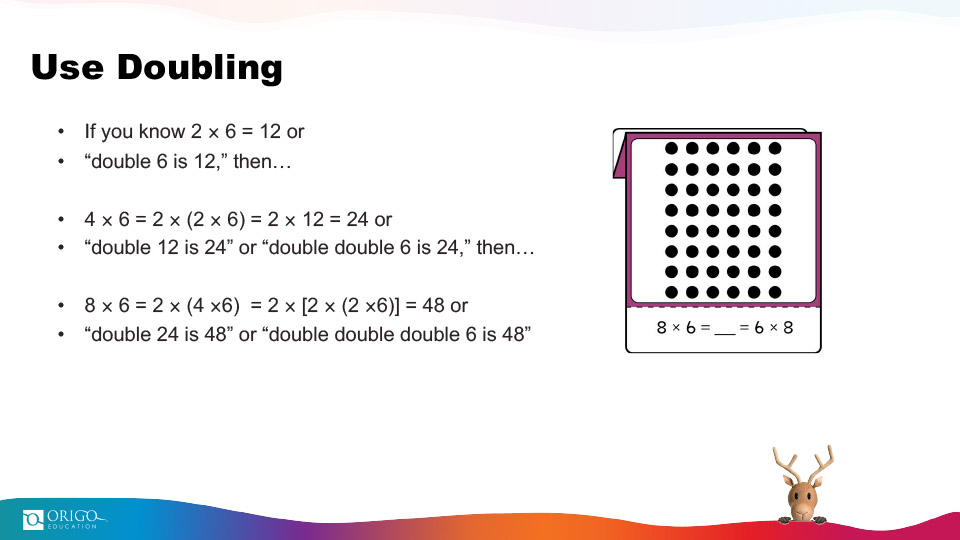
Extending Doubling
Multiplying by 10 is easy, since the unit changes from a place value of ones to a place value of tens. PLEASE don’t tell kids “to just add a zero” since that doesn’t always work (1.5 x 10 is not 1.50 but rather 15). It’s important that students think about multiplying by 10s as a place value shift.
Using doubling, I can look at the equation of 6 x 5, which might be difficult for some students to process mentally, but they might know 6 x 10 = 60 (six tens) and that by halving 60, they arrive at 6 X 5 = 30. To further explore the double & halve strategy, look at the charts below:
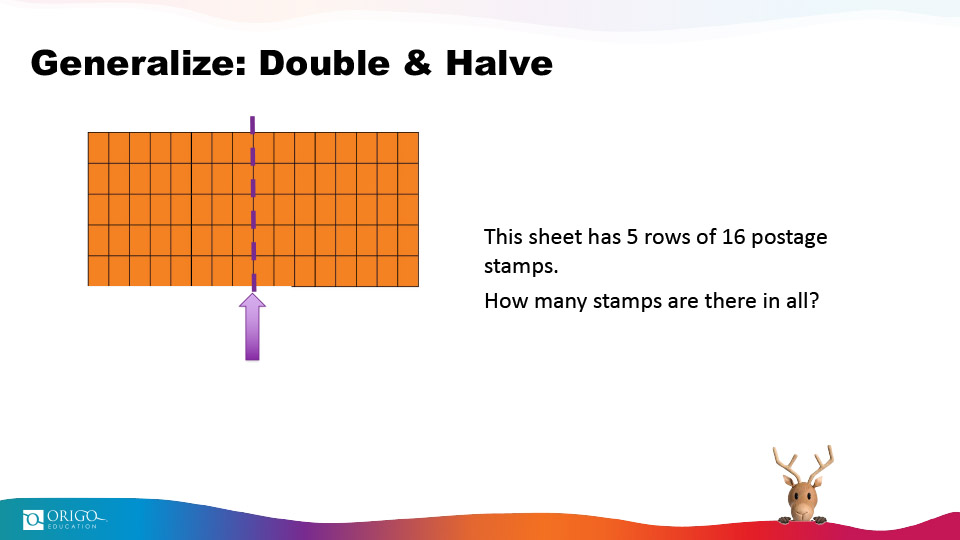
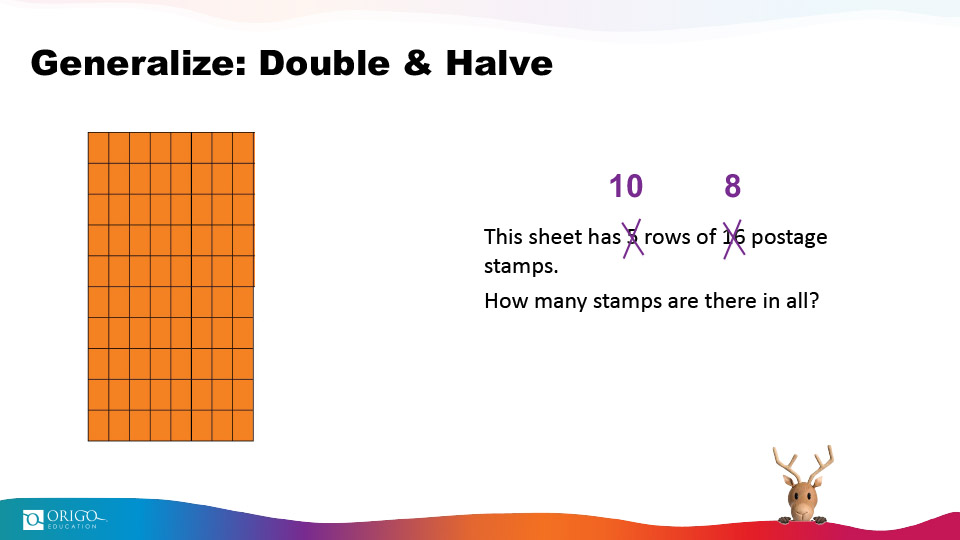
By halving the sheet, students are able to work with the number 10 (instead of 5) and arrive at the answer more efficiently.
Doubling and halving is a very handy strategy as it can allow students to work with “friendly” numbers. For instance, 15 x 12 might pose a challenge, but by halving the 12 (6) and doubling the 15 (30), the problem instantly becomes more accessible, 6 x 30 = 180 as does 15 x 12.
One of the hallmarks of a good strategy is that it can be used with greater numbers. Doubling and halving work equally well with fractions.
1 ½ x 6 = 3 (double ½) x 3 (halve 6) = 9
Generalizations
Thinking about multiplication as equal groups—five flowers in six different vases or four kids each in seven teams—makes it easier to explain and understand the concept of multiplying by 0. If there are no groups of vases or no groups of teams, no matter how many flowers or how many kids, then we have 0 groups. So, zero X any number is always zero, because we don’t have any groups. Similarly, if there is only one vase of five flowers or one team with four kids, one X any number is always that number (or a single group).
Building Down & Building Up
If students know their “ten fact”, they can easily figure out a related nine fact. For instance, a student may not know 9 x 3, but they do know that 10 x 3 is 30 and that 9 x 3 is one fewer group of three, therefore 10 x 3 = 30 – 3 (one group of 3) = 27. By building down, they arrive at the accurate response to 9 x 3 = 27. They could solve 8 x 3 in the same way, by building down twice. They know that 10 x 3 is 30 and 8 x 3 is two fewer groups of three, therefore 10 x 3 = 30 – 3 = 27 – 3 =24.
And of course, you can build up. Students may not know the answer to 6 x 6, but they know that 5 x 6 = 30. They can add one group of 6 to get the answer, i.e. 30 + 6 = 36 = 6 x 6.
And like any good strategy, it can be extended to more complex numbers. Building down and building up work equally well with decimals
Building down example: 4.2 x 6 = (4 x 6) + (2 x (0.1 x 6)) = 24 + 1.2 = 25.2
Building up example: 1.9 x 5 = 2 (building up) x 5 – (0.1 x 5) = 9.5
So, with four strategies—doubling & halving, generalizations, building down, and building up—we’ve provided students with the number sense and reasoning they need to successfully tackle multiplication and division. How much easier is it to ask students to learn four strategies as opposed to memorizing a multiplication chart, which won’t help when they start working with fractions and decimals.
So, what about memorization?
Traditionally we taught students to memorize their times tables. In fact, I remember that when I was in third grade I was handed a deck of flash cards which I dutifully memorized, but didn’t truly understand, and certainly didn’t remember when questioned months later. But memorization as an initial instruction strategy remains prevalent in classrooms and homes across the county. However, research shows that long-term learning through memorization alone simply doesn’t work. But that same research tells us that memorization (or knowing something from memory), when used at the end of instruction, to consolidate learning dramatically increases student learning. Even knowing these four strategies, students might still struggle with facts like 6 x 9 = 54 and 7 x 8 = 56, especially when building towards automaticity. A more deliberate memorization might be helpful at this time as a move towards efficiency.
The conclusion is that teaching with strategies helps students not only achieve the accurate answer efficiently, but even more important, helps them understand the math behind the problem and which strategy will be best help them solve the problem at hand.




