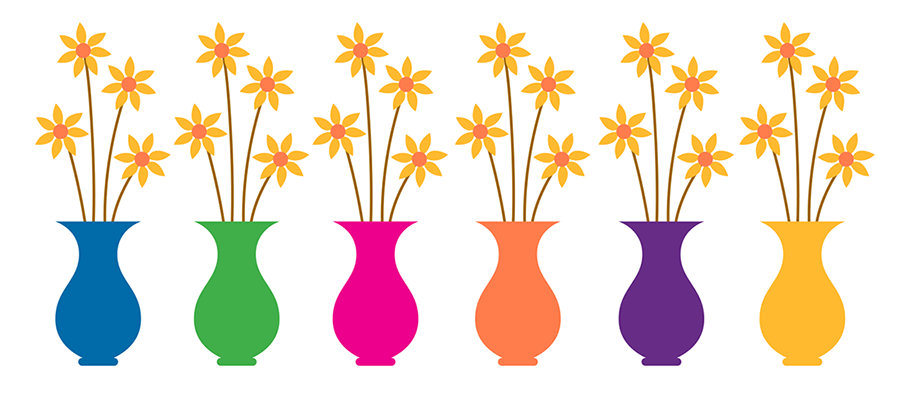Number Sense and Place Value
Differentiation or Intervention in Math Instruction?
What’s the difference and what should core math instruction look like?
Recently I was working with a school district in Massachusetts that had begun to implement a new math program. Teachers were doing well with the basics of the program using a Math Workshop framework; however, they were struggling with how to support all students in their classroom including students identified for intervention.
The instructional leaders in the district noticed a need for supporting teachers with understanding the difference between differentiation and intervention. Since we were focusing on core classroom instruction, we decided to address what instruction looks like in the regular classroom and the differentiators between the two instructional approaches.
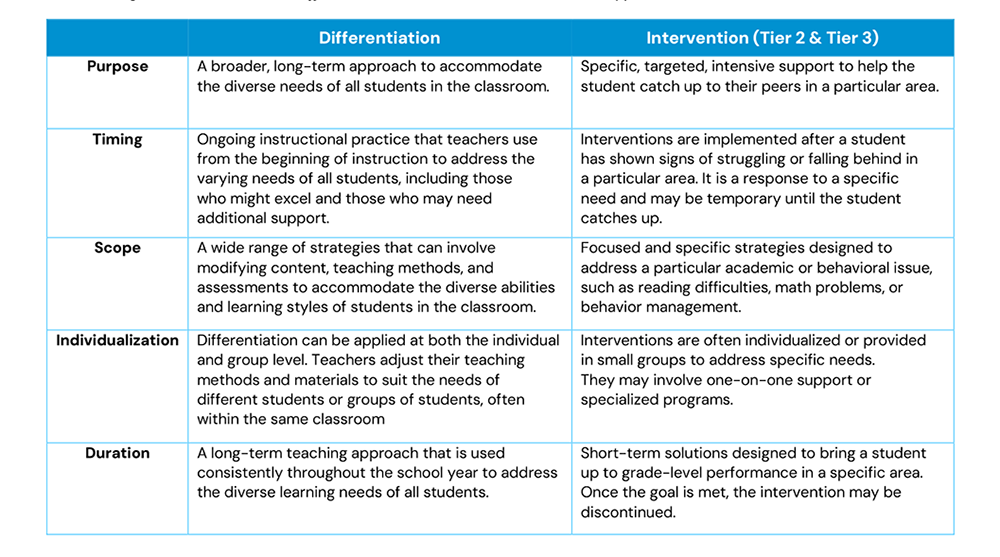
After identifying the differences, we summarized intervention as a targeted, short-term strategy to address specific academic challenges, while differentiation was defined as a broader, long-term approach to accommodate the diverse needs of all students in the classroom. When thinking about how we defined both, we determined teachers needed:
- A clear idea of classroom differentiated support
- How to use formative assessment to identify when students were struggling
- A framework to provide differentiation to prevent future learning loss
The resulting professional learning session provided a framework for a targeted professional learning session on inclusive classroom instruction. We explored this Grade 3 lesson as a model for this approach. Teachers may use this template when planning instruction. This lesson was modified from ORIGO Stepping Stones 2.0, Grade 3, Module 1, Lesson 7.
Learning Target Students will represent and solve problems involving multiplication.
Prerequisite Concepts Repeated addition
Warm-up One way to identify students who may struggle with a concept, is to start with a number sense activity to activate prior knowledge. In general, 80% of the students in class should be able to complete the activity with success. The teacher can formatively observe student performance to determine which students may have difficulty with the concept. To do this, teachers need to identify the learning target for the lesson and the prerequisite skills students need to be successful.
Warm-up Number Sense Activity (10 minutes)
There are 4 flowers in each vase. There are 6 vases. How many flowers are there in total? (repeat with 3 other similar problems)
This problem enables the teacher to see how students represent the problem. Are they using repeated addition? Can they illustrate the problem? Can they solve the problem using manipulatives such as cubes? This 10-minute number sense activity enables the teacher to see which students have the prerequisite skills necessary to understand multiplication. It also enables the teacher to determine which students may need some differentiated support related to the learning target within the lesson.
Teaching the Mini-Lesson (20 minutes)
The teacher then takes the same examples from the number sense activity and prompts students to identify the repeated addition for each of the problems. For the example above, the problem would be 4 + 4 + 4 + 4 + 4 + 4 = 24 pointing out that this is a really long equation as repeated addition. The teacher models the equation represented as 4 x 6 = 24.
The teacher then asks students to match each word problem from the initial activity with its matching multiplication equation and prompts students to model their thinking with cubes and write the equations.
Student Independent Work and Teacher Differentiation (20 – 30 minutes)
After the teacher has modeled and prompted students to collaborate and create matching equations while representing these equations using manipulatives and illustrations, students move to a station rotation model. The table below illustrates the rotation model for this lesson. In this model, students go through 2 – 3 learning stations.
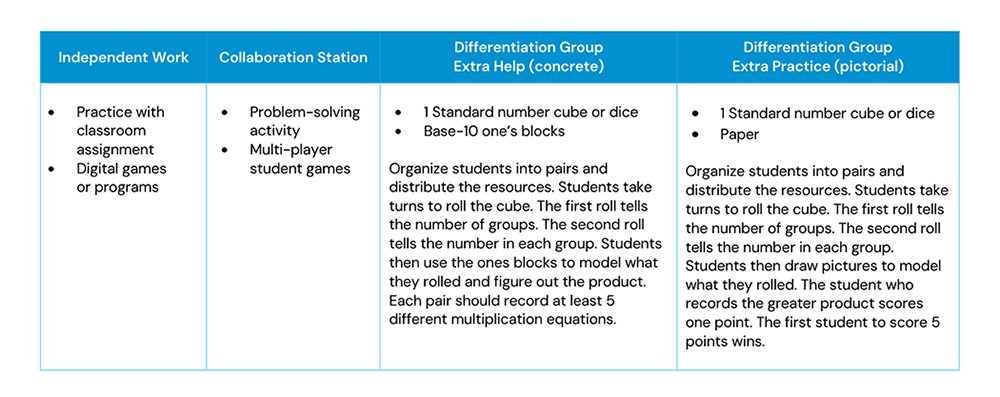
During the differentiation stations, the teacher observes if students need additional support in subsequent lessons or if there may be additional gaps in student learning.
Reflecting as an Exit Ticket (5 – 10 minutes)
After station rotation, the teacher invites individuals to draw pictures and write the independent work equations on the board. As the problems are discussed, the teacher asks students to explain their thinking. In addition, the teacher asks questions that focus on thinking on the number of equal groups, the number in each group, the product, and how each connects to the equations.
As the exit ticket, the teacher projects a picture problem as shown below and asks students to think of a word problem and multiplication equation to match the picture. This becomes their “exit ticket.” The teacher can collect these or walk around and observe whether students are getting the concept or may need additional support. Based upon the exit ticket, the teacher can plan for tomorrow’s differentiation groups.