Cal's Corner
Focus on Fractions: How Do Children See and Use Fractions from the Ancient World?
This is part of a series on fractions:
- Part 1: This post – History of Fractions and Fraction Concepts
- Part 2: Fractions Facts
- Part 3: Fraction Models and Visuals
- Part 4: Decimal Fractions and the Number Line

Sundial in a flower garden.
Some initial timely thoughts to use fractions.
When fractions are mentioned in relation to the mathematics curriculum, most adults think that these mysterious numbers are the responsibility of teachers in upper grades (about Grade 4 onward). But, if we step back and think about the idea to use fractions rather than the symbolic manipulation, young children do frequently work with these numbers. For them, it is natural to share a collection of items and talk about the part that each received. As they work with objects, early learners begin to build their fraction language using the term half and very often quarter. With the right experiences young students might be able to use more language and in turn, develop a greater understanding of this set of numbers.
Influence and History of Fractions
Historically, fractions (or at least the need for fractional parts) appeared very early and had tremendous influence on the overall developments in mathematics that we still use today. Over 4,000 years ago the civilizations were wrestling with describing amounts after a collection had been shared. It was challenging, so cultures like the Ancient Babylonians worked around the difficulty by developing a number system that did not require as many fractions as the base-10 numbers we use today. In the Babylonian base-60 system, dividing by 2, 3, 4, 5, or 6 (as well as 10, 12, 15, 20, 30, and 60) gave answers that could be interpreted and expressed in a meaningful way.
The history of fractions is everywhere around us! Today when children look at an analog clock,1 they see the remnants of an ancient system which allows them to break one hour into a whole range of fraction parts, not just halves and quarters.2 A later blog will describe how the number line helps children learn fractions. The number line can be viewed as an unwrapping of the circular minute segment around the clock face so the two ideas (a number line and minutes around a clock face) are connected.
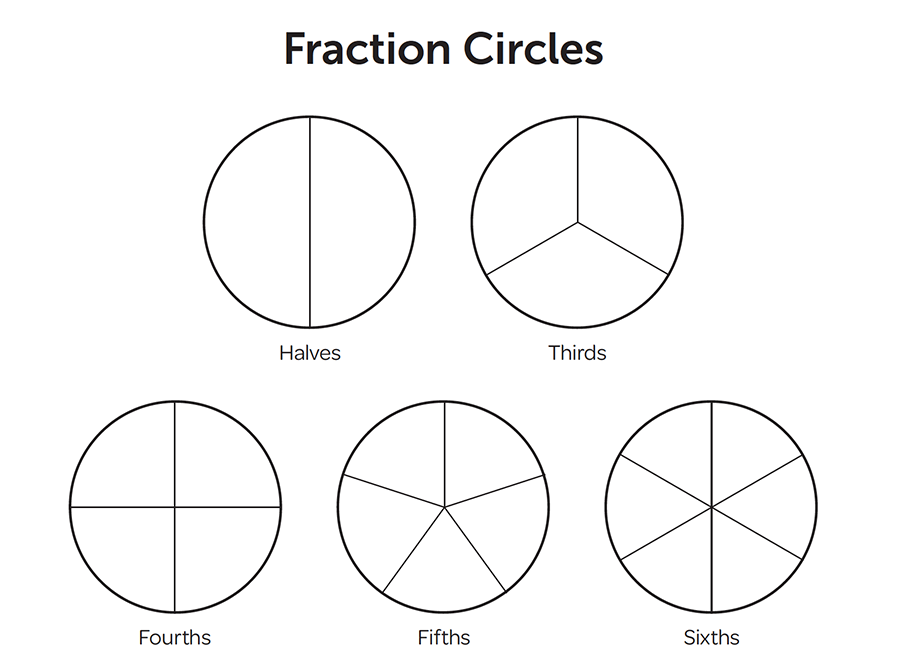
All ancient civilizations wrestled with time and breaking the day into parts. The Romans used sundials borrowed from the Egyptians and split the daylight hours into 12 parts. The choice of 12 allowed them to work with halves, quarters, thirds, sixths, and twelfths. This convention is, of course, still in use today. Work with minutes and hours, taken together, show some basic fractions such as 1/2, 1/3, 1/4, 1/5 and 1/6, as shown with the fraction circles below.
Fraction Concepts – Why Do Students Struggle?
Several reasons are cited why students struggle with fractions (Van de Walle, J.A et al. page 291).3 These include the failure to provide conceptual understanding as well as overgeneralizing by students from work they have completed with whole numbers. Using a greater range of language that is generated from pictures that relate to a clock face might help students as they begin their journey to learn about fractions as well as time. Young children will benefit from more frequent and earlier work with the correct types of activities that can sequentially build on what they bring to school.
The next blog will describe why an in-depth knowledge of fractions is essential for later mathematics. The blogs that follow will describe strategies that will increase the chances that the necessary success with appropriate concepts and skills involving fractions can be achieved.
1 The analog clock is a vital visual model in the development of a child’s understanding of time as well as fractions. It is practically impossible to see fractions on a digital clock.
2 In a modern digital world, billing often occurs in tenths or quarters of an hour, scheduling is broken into sixths or quarters, and appointment programs are written for 5, 10, 15, 20, and 30-minute intervals. These time intervals can be used with students to show twelfths, tenths, sixths, fourths (quarters), thirds and halves.
3 Van de Walle, J., Karp, K., Bay-Williams, J. 2013. Elementary and Middle School Mathematics: Teaching Developmentally. Boston: Pearson
Click HERE to view and download the resource for this article!
In my next blog, we will discuss how fractions are key to a child’s future success in mathematics.




